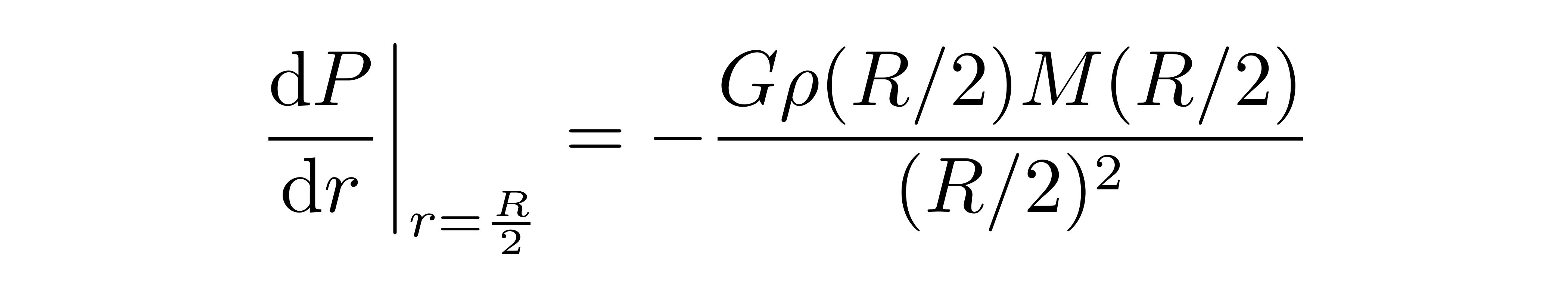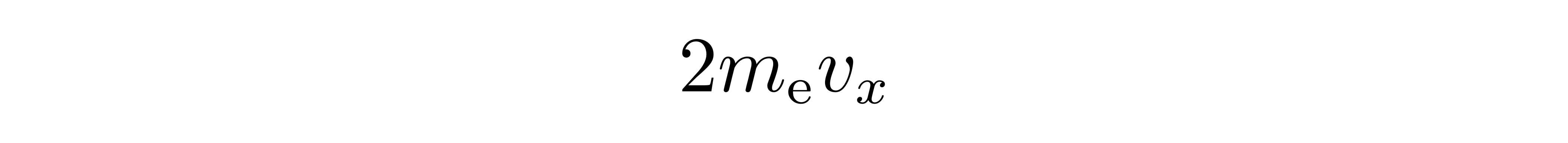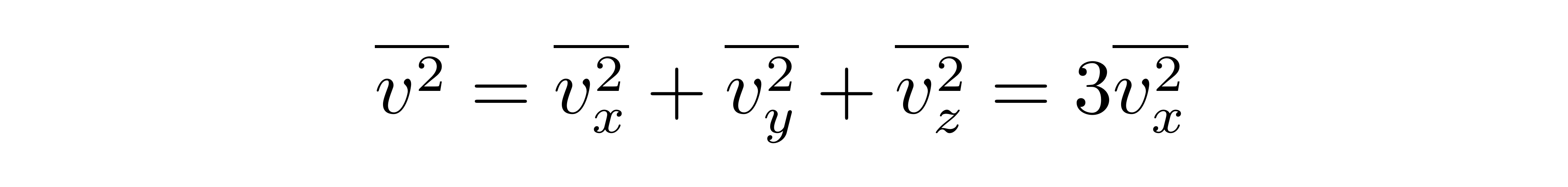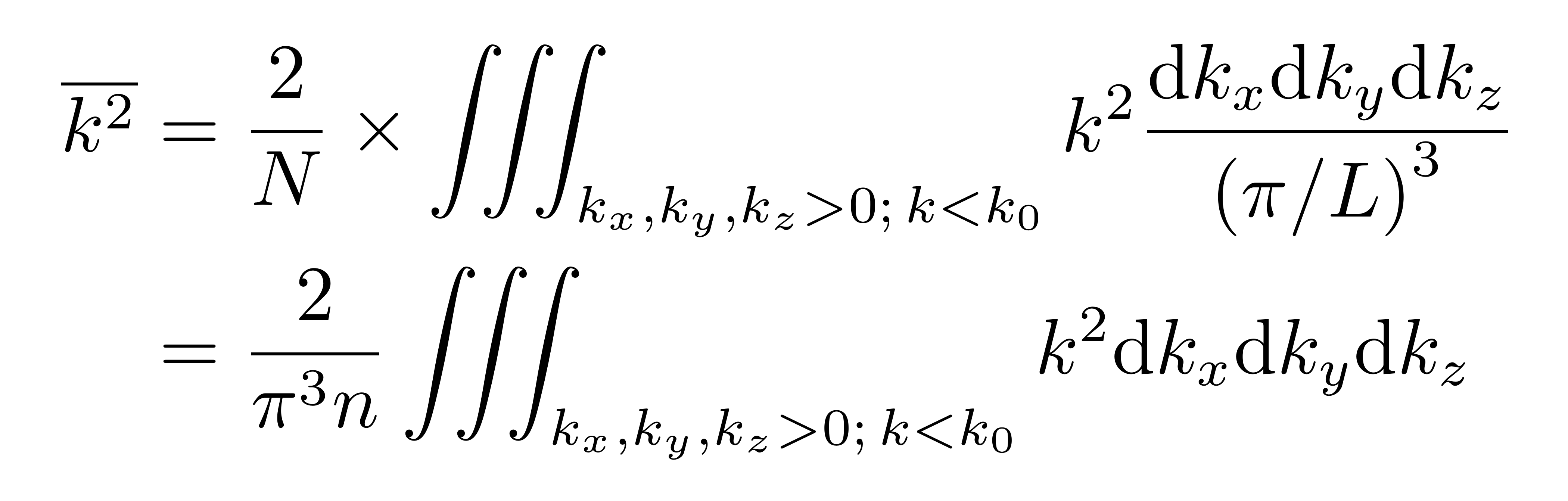sports bets for today

当M大于1.44倍太阳质量且小于3倍太阳质量时，恒星最后会成为中子星。如果M大于3倍太阳质量，那么恒星会成为比中子星更致密的星体（比如还存在于假设阶段的夸克星）甚至会变成黑洞。在这次直播课中，张朝阳将分析近零温电子气体的压强以及估算白矮星中心处的压强，最后推导出白矮星的质量上限，也就是钱德拉塞卡极限。

描述星球内部压强的方程是流体静平衡方程。在星球内部取一个底面积是dS，高是dr的柱状微元，柱状微元的母线与星球的径向平行，微元到星球中心的距离是r。在径向方向，微元受到三个力的作用：星球内部物质对微元的引力、微元上下底面受到的压力。

另一方面，均匀球壳不会对其内部质点有引力作用，因此微元受到的引力只来源于半径小于r处的物质。设距离中心r处的密度为ρ(r)，距离中心小于r的物质总质量为M(r)，微元上底面压强是(P+dP)，下底面压强是P，取沿径向指向外的方向为正方面，前述三个力满足的平衡条件为

简单运算一下可以将上式化简为

消去dS，并写成导数形式可得

这就是星球的流体静平衡方程，其中的压强表示星球处于静平衡时的压强。如果星球内部物质所提供的压强小于这个方程给出来的压强，那么这个星球会被引力进一步压缩；如果内部物质提供的压强大于这个方程给出来的压强，那么这个星球会反抗引力的压缩而向外膨胀。

假设白矮星半径为R，在白矮星表面，因为没有外部的力压迫星球表面物质，因此表面的压强P(R)=0。当半径r趋向于零时，物质密度ρ(r)趋向于白矮星中心密度ρ(0)，由于白矮星内部物质没有被无限压缩，因此ρ(0)是一个有限值。当r非常接近零时，有

所以当r趋向于零时有

这说明压强随半径变化的曲线在r=0处的切线是平行于r轴的。换言之，随着半径r从零变化到R，压强从一个有限值P(0)缓慢下降了一小段，然后再较快速地下降到0。假设白矮星中心处的压强为Pc，采用线性近似，可以得到

另一方面，根据流体静平衡方程，有

对于密度均匀的星球，M(R/2)会等于M/8。但是，星球的密度一般不是均匀的，而是内大外小，因此M(R/2)往往大于M/8。在这里，将M(R/2)估算为M/3，并将ρ(R/2)估算为白矮星的平均密度，于是上式可以近似为

与前面的结果结合可以得到

化简即得

这是白矮星中心处压强的估算值，只有在白矮星处于平衡状态的时候才成立。前面也提到了，白矮星内部由电子气体的压强来抵抗引力压缩。如果白矮星中心处的电子气体压强小于上式给出的压强，那么这个白矮星会被引力进一步压缩；如果白矮星中心处的电子气体压强大于上式给出的压强，那么白矮星将会在过大的电子气体压强的作用下膨胀。只有在电子气体压强等于静平衡方程给出的压强时，白矮星才会维持平衡。

从无限深势阱中的粒子出发 分析得到电子气体简并压

为了得到电子气体简并压，需要分析电子气体的物态方程。物态方程由物质的宏观量（体积、温度、压强等）给出，是不依赖于物质所处的容器的。比如理想气体，可以在方形盒里边推导理想气体的物态方程，这样得到的物态方程适用于处于任何容器的理想气体。同样，可以在无穷深方形势阱里边推导电子气体的物态方程，将其用到白矮星内部的电子气体中。

电子是费米子，满足泡利不相容原理，因此即使不考虑热激发，电子都不会全部处于最低能级，而是从最低能级一直往更高的能级“垒上去”，直到所有电子都被排列完毕。由于电子自旋可以取两个不同的值，因此电子能级的简并度为2，换言之，每个能级其实可以放下两个电子，再多的电子就会破坏泡利不相容原理了。

在不考虑热激发的情况下（也就是零温情况下），电子会依次从最低能级往高能级排布，直到所有电子都被排布完毕。由于白矮星内部电子实在太多了，需要排布到很高能级才能把电子排布完。当温度大于0开尔文时，这些电子中的一部分就会被激发到更高的能级，热激发导致单个电子多出来的能量约为k_B*T量级，这里的k_B是玻尔兹曼常数。

虽然白矮星内部温度很高，但是这部分热激发能量与电子在零温时排布的最高能级比起来还是很微小，因此白矮星内部的电子气体完全可以被当成零温的来处理。

张朝阳在以往物理直播课中介绍过处于一维无穷深势阱的粒子的第n阶能级的波函数为

其中k=nπ/L，相应的能级为

对于三维方形无穷深势阱，相应的能级为

其中ex，ey，ez分别是直角坐标系的三个基矢，nx、ny、nz是三个量子数，只能取正整数值。

气体的压强的微观来源是粒子对容器壁的碰撞，电子气体的压强来源也是类似的。由于压强是各向同性的，因此可以通过分析任意方向的面在单位时间内所受到的粒子碰撞力来求出压强。假设容器壁垂直于x轴，电子气体处在x负方向那一侧，在x方向具有速度分量vx>0的电子才能碰到这块容器壁，碰撞之后x方向的速度分量变成了-vx，因此这个电子的动量改变量为

式中的m_e是电子质量。设具有速度分量vx的电子数密度为n_{vx}，容器壁面积为A，那么单位时间内碰撞到这块容器壁的具有速度分量vx的电子数为

这些电子提供给容器壁的压力为

将这些力加在一块，然后除以面积A即可得到压强：

其中v_x^2上的一横表示平均值，n是电子数密度。考虑到各向同性，可以得到

于是

上式最后一步使用了动量与k的关系p=ℏk以及动量与v的关系。

根据三维无限深方形势阱的粒子能级，可以知道在k空间的第一象限，每个能级对应于大小为(π/L)^3的体积，因此有

其中的因子2来源于电子的自旋，除以总粒子数N=nL^3就对应于平均操作，式中的k0是从最低能级向上依次排布完所有电子后所对应的最大的k。将上式代入压强公式可得

接下来还需要求出k0。由于k0是从最低能级向上依次排布完所有电子后所对应的最大的k，因此可以通过在k空间积分求出排布到k0时总电子数：

由此可得k0为

将k0的表达式代入压强表达式可得

这就是电子气体在近零温的情况下的压强，它与电子数密度的5/3次方成正比，与电子质量成反比。

电子气体简并压与引力平衡 估算白矮星半径

接下来分析需要将电子气体的简并压用白矮星的质量、半径表示出来。从这里开始，将白矮星静平衡所需的中心压强记为Pg，白矮星中心处的电子气体压强记为Pd，根据前面的分析，有

假设白矮星中心处的电子数密度是平均电子数密度的α倍。由于白矮星的密度是内大外小的，所以张朝阳假设α=4。实际上，如果采用线性近似的话，中心数密度确实正好等于平均数密度的4倍，因此α=4是一个很合理的假设。

由于恒星在成为白矮星之后氢燃料被消耗得所剩无几了，白矮星内部大部分都是重核，其质子数和中子数基本相等。由于电子数与质子数相等，因此电子数密度约等于核子数密度的一半，所以，白矮星中心处的电子数密度为

将其代入电子气体的简并压公式，可以得到中心处电子简并压为

又因为

所以有

当质量M固定时，Pg随半径R的四次方衰减，而Pd随半径的5次方衰减。容易知道，无论质量M取何值，Pg与Pd两者关于R的曲线存在一个交点，对应半径R0，如下图所示：

当R<R0时，Pd>Pg，换言之，中心处的电子简并压大于维持流体静平衡所需的中心压强，因此这个白矮星会被电子简并压推着往外膨胀，从而R会变大；当R>R0时，Pd<Pg，因此中心处的电子简并压小于维持流体静平衡所需的中心压强，这时候电子简并压无法承受引力的压缩，因此白矮星会进一步缩小，从而R会变小。

从这里的分析可以知道，白矮星最终会稳定在R=R0处，因此Pg与Pd两曲线交点对应的半径R0就是白矮星的半径，由Pd与Pg的表达式可得R0满足的条件为

所以

这就是白矮星半径的估算值。将一个太阳质量以及α=4代入上式，可以知道此质量的白矮星半径约为10km。

考虑相对论电子气体 推导钱德拉塞卡极限

根据前面的分析，无论白矮星质量M等于多少，白矮星都能稳定存在，这明显是不对的。问题出在哪里呢？张朝阳告诉大家说，问题出在前面计算电子气体压强时没有考虑电子的相对论效应。电子气体的压强本质上是电子对容器壁的碰撞所导致的力的现象。在同样的动量大小下，碰撞粒子数越多，所表现出来的压强越大。

但是，碰撞频率正比于粒子速度，而在相对论的情况下，因为粒子质量变大了，所以具有特定动量的粒子所对应的速度是小于牛顿力学情况下的具有相同动量的粒子所对应的速度的，因此在相同动量情况下，用牛顿力学来计算的粒子碰撞频次高于用相对论来计算的碰撞频次，最终就会导致用牛顿力学计算出来的压强偏大。

为什么需要考虑电子的相对论效应呢？这是因为当白矮星被压缩得很小时，电子密度很大，从而电子在k空间堆积出来的1/8球体的半径k0会变得很大，换言之其中有大量的电子具有非常高的速度，所以必须在狭义相对论的框架内考虑这个问题。

在以往直播课中张朝阳已经通过克莱恩-高登方程说明了相对论性粒子的k空间与非相对论情形相同，唯一的区别就是相对论情形的电子质量将依赖于k，因此前面对电子气体的表达式需要改写为

根据质能关系，我们有

由此可得

所以

如果考虑极端相对论情形，此时k0非常大，因此式中k比较小的部分对积分的贡献可以忽略不记，只需考虑k很大的那部分，此时被积函数的分母可以近似为k，这样的话就可以得到

重复非相对论情形时的分析，可以估算得到中心处的电子简并压为

需要强调的是，因为前面使用了k0远大于a这个近似条件，所以这个式子只在R很小的时候才成立，它表示的是在质量M保持固定时，半径R趋向于0时白矮星中心处的电子简并压的变化情况。

对于R比较大的时候，k0远大于a这个条件不再成立。特别的是，当R很大时，电子数密度n很小，这时候电子气体退化成非相对论电子气体，其简并压满足的是正比于1/(R^5)的关系。将这里的讨论总结起来就是：

而不管R是大还是小，维持白矮星平衡所需的中心压强都是

如果在R比较小的时候，Pg小于Pd，当R变大之后，Pd先以1/(R^4)的速度下降，然后以1/(R^5)的速度下降，而Pg保持以1/(R^4)的速度下降，最终Pd必小于Pg，因此在压强-半径坐标系上，Pd与Pg曲线必定相交，这样的话白矮星能够维持平衡，平衡点就对应着Pd与Pg曲线交点。

如果在R比较小的时候，Pg大于Pd，当R变大之后，Pd先以1/(R^4)的速度下降，然后以1/(R^5)的速度下降，Pg保持以1/(R^4)的速度下降，可见Pg曲线永远在Pd曲线上方，它俩没有相交点（如下图所示），因此无论半径为多少，电子简并压都无法提供足够的压强抵抗白矮星塌缩。

从前面的结果可以看到，Pd正比于M^{4/3}，Pg正比于M^2，因此当M增大时，同一个R下的Pg增长速度大于Pd的增长速度。因此，只要M足够大，Pg将会大于Pd，于是这个质量对应的白矮星将无法稳定存在。那白矮星的临界质量是多少呢？临界质量对应于Pg正好等于Pd时的质量，换言之

由此可以得到临界质量满足

代入相关数值，可得

这就是钱德拉塞卡极限，大约是1.5倍的太阳质量。这里的结果是近似得到的，因此与实际结果存在一点差异。精确计算的结果表明白矮星质量上限大约是1.44个太阳质量。

据了解，《张朝阳的物理课》于每周周五、周日中午12时在搜狐视频直播，网友可以在搜狐视频“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频。此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。

vegas online bettingplay baccarat online for real moneyncaa betting lines football

---

声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。