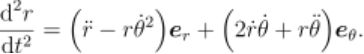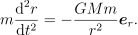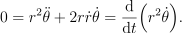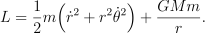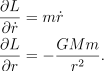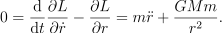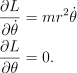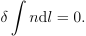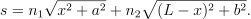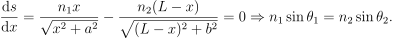The half-circle section below the authentic zipper has a bigger outline in comparison to the counterfeit one.
The counterfeit brand would have made the bag more practical if it used smaller details but decided not to do so.
BetMGM Online Casino Bonus
A search filter lets players conveniently display blackjack games separately from other types of games.
win win online betting It's going to take a little while, with the tech giant, a new platform-led platform designed to make the internet one of the most popular in the world.
.
如何理解 Lagrangian

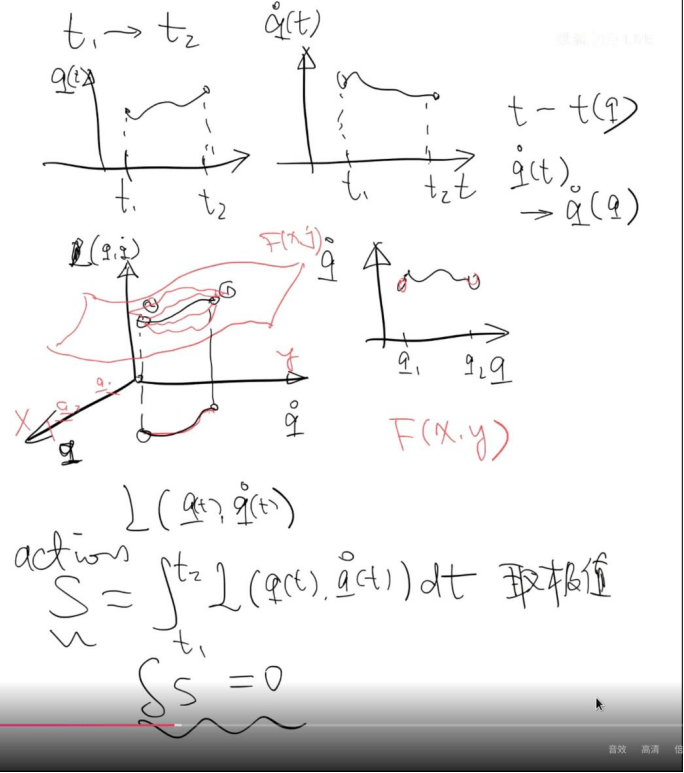
在 Lagrange 力学中,一个力学系统的所有信息都通过一个被称为 Lagrangian 的标量函数来进行概括。以一维不含时系统为例,它的 Lagrangian 可以写为广义坐标 q 及其对时间导数的函数:

而最小作用量原理说的就是在确定了系统运动的初末点的时刻和坐标之后,在这之间真实发生的运动应当使得作用量积分
![]()
取到极值。像这样的关于某条具体的路径 q(t) 求解某个目标函数极值的问题在数学中被看作变分问题的实例进行处理,而这类问题的结果是发现极值路径需要满足 Euler-Lagrange 方程。而在力学中,如果取 L = T - V,那么对应的 Euler-Lagrange 方程将会和 Newton 力学的动力学方程保持一致。其中 T 是系统的动能,而 V 是系统的势能。
更好地来理解这件事情是如何进行的,人们可以将广义坐标 q 和它对时间的导数(广义速度)——注意每给定一条路径,这两个量对于时间的关系就确定了——画在一个平面上,因此这样的平面上的线也就标记了这样路径的形状。
![]()
由于 L 是广义坐标和广义速度的函数,因此这样画出来之后,每一条路径上的 L 的值都可以相应地进行计算,而作用量 S 就是沿着路径把得到的这样随时间变化的 L 值当作是时间的函数进行积分。力学规律就像是有一个跳出世界之外的神,祂不断摆弄起点和终点之间的可能路线,找到一条让 S 的值取得极值的(通常是最小值)的路线,而这条路线就是实际世界中发生的运动轨迹。
中心力场问题
可以使用中心力场中质点的运动这一问题来演示实际应用 Lagrange 力学方法处理问题的步骤。首先来重复一遍 Newton 力学的处理。中心力场中的质点的位置描述仍然取极坐标 (r, θ) 来实现,那么其位置对时间的二阶导数有(注意极坐标基向量随位置的变化)
![]()
这也正是质点的加速度。如果中心力场是 Newton 的引力场,那么动力学方程就可以写为
![]()
整理就得到了两个方向的分量方程:
![]()
在角向方程两边同乘 r 我们很容易构造一个守恒量(正对应角动量守恒)
![]()
接下来考虑使用 Lagrange 力学的手段来获取动力学方程。如前所述,系统的 Lagrangian 应该有动能减势能的形式,即
![]()
首先来检查径向分量,计算 Lagrangian 的一些偏导数有
![]()
那么有 Euler-Lagrange 方程
![]()
然后是角向分量,有
![]()
从而有
![]()
按照最小作用量原理,这两个方程就确定了中心力场中粒子的实际运动轨迹(动力学方程)。不难看到它们和 Newton 力学的处理是完全一致的,而且在 Lagrange 力学中角向的角动量守恒方程立即得到,而不再需要观察方程形式积分获得。
Fermat 原理
将物理学规律表达为实际路径使得某个量取极值的做法并非 Lagrange 力学的首创。事实上比 Lagrange 早100多年,Fermat 就已经意识到几何光学中光线的实际传播轨迹对应着某个量取得极值,这种同力学中的作用量相近地位的量被称为光程。其数学表达可以写为
![]()
其中 n 代表空间各处的折射率,而积分变量 dl 为光行走路线上的元弧长。这个极值问题不同于 Lagrange 力学,它要求光的起终点位置确定而并非位置和时间。ndl 的积分也被称为光程。而 Fermat 原理的表述正是固定起终点的情况下,光在其间走的实际路线(光线)为使得其光程最短的那条路线。如果考虑到介质中光的相速度 v = c/n,那么也可以将 ndl 理解为 c dl/v 正比于光通过这段线元的时间,因此 Fermat 原理也经常被表述为 “光线传播的路径是所需要时间最少的路径” 这样的最短时间原理。虽然历史上 Fermat 原理提出的时间更早,但是理解了 Lagrange 力学之后再回过头来看 Fermat 原理或许能带来更多的启示。在量子论提出以前,人们倾向于认为光是一种波动。而今天人们清晰地从 de Broglie 关系理解了光作为波同时也拥有粒子的特性。折射率所决定的光程同光的相位,动量都紧密地联系在一起,让 Fermat 原理的内涵更加丰富,而光的本质至今仍是物理学中最古老同时也最前沿的课题之一。
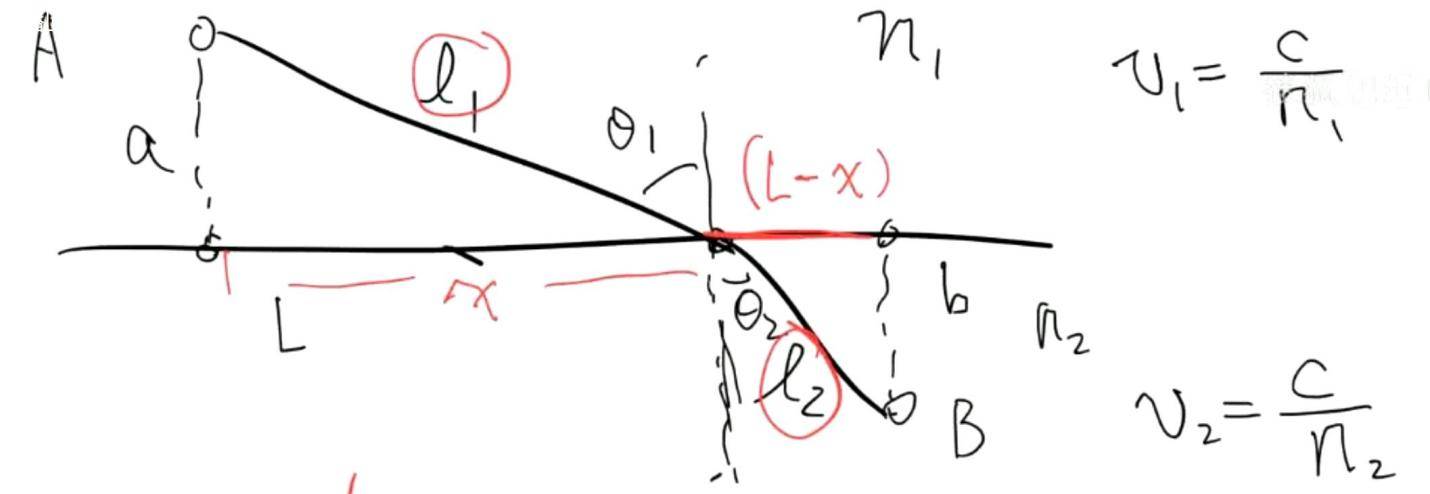
Fermat 原理可以被用于论证光通过介质表面时的折射定律。这里来演示这个问题。首先需要明确在均匀介质中,由于 n 是个常数,因此它可以提到积分号外边。于是光的路线作为两点之间最短的路线应当是直线。现在来考虑两个均匀介质之间存在平面界面的情形:
![]()
令 L 代表AB两点连线在界面上投影的距离,由于光在均匀介质中沿直线传播,因此决定光的实际路径的参数只有其路线同界面的交点。不难看到,取最短路径只发生在该交点同A, B向界面的垂线所确定平面内。故,如图,取交点同A到界面的垂线垂足距离为 x, 光程可以写为
![]()
计算这个函数关于 x 的极值,可以通过找它对 x 的导数的零点实现,有
![]()
而这正是折射的 Snell 定律。
据了解,《张朝阳的物理课》于每周五,周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
best thursday night football prop betsis online betting legal in ussports betting age
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。